Quad Trees: Nearest Neighbour

This article is the third one in a series exploring Quad Trees. If you haven’t read previous ones, I highly recommending starting with Introduction to Quad Trees.

Introduction to Quad Trees

Let's implement quad tree in TypeScript!

In the second article we explored how we can get all elements in a given area, but sometimes we might need to find the closest element to our target. In contrast to our previous operations like inserting and finding in a region, as we don’t know in advance which region our resulting point is going to be in. If our tree is sparse, we might end up in an area on the other side of the tree. And if there’s plenty of points close to our target, we don’t want to explore all neighouring regions. We need to use some trick and traverse the tree in a smart way.

Solution

Our solution is based on two observations:

• there’s a higher chance to find nearest element in a region close to our point than in a region far from our point. This does not guarantee that the closest element is going to be in that region but can give us some extra information
• once we find potential closest point (with distance k), we can ignore all points which are further than k.

These two observations can lead us to a very effective way of traversing the tree.

Initially we start with no closest element so we visit the region closest to the point in question. Eventually we will find a point. This might not be the closest element, but we know whatever comes next can’t be further than the distance to it. Let’s call this distance k. Now when inspecting new regions:

• we can reject any region which closest point is further than k
• if the region’s closest point is less than k, it potentially can have closest point. We can inspect the region recursively.

Below is an example visualising the solution above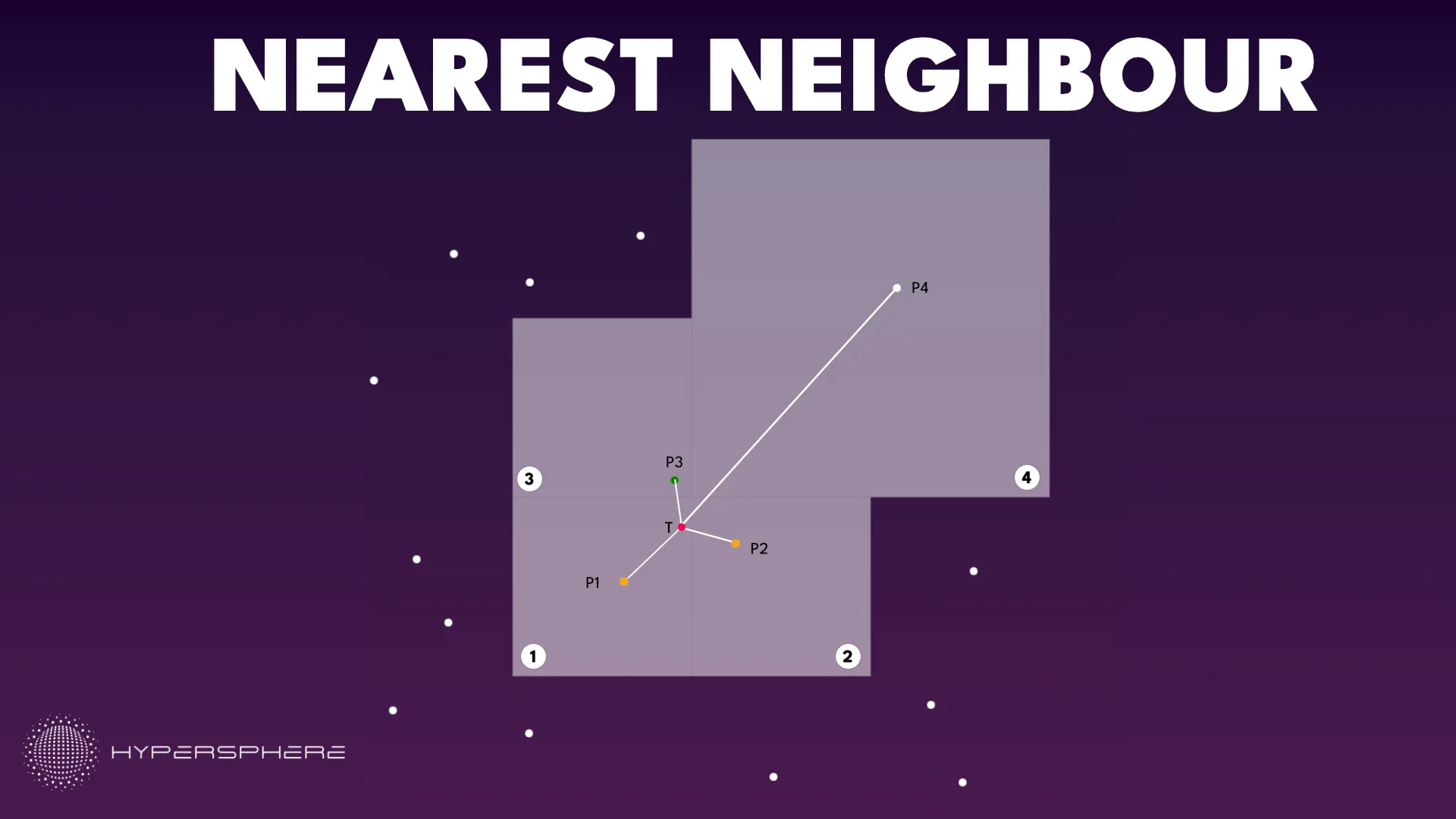

We want to find the point closest to T.

1. We start by visiting region (1) as it’s the most promising. We find P1 which distance is better than already stored (as we didn’t find any point yet).
2. We visit another region: (2). Point P2 is closer to T than P1 so we update the distance to it.
3. We visit (3) as distance to this region is still lower than distance between T and P2, so there might be potential points minimising our distance. We find P3 which is closer to T than P2. This is our new distance.
4. We visit (4) as the distance to this region is less than distance from T to P3. We find point P4 but it’s not closer than our minimal distance.

Any other region we investigate is further so our result is P3.

Implementation

findNearestNeighbour(p: Point) {
        return this.findNearestRec(p)

private findNearestRec(p: Point, distance: number = Infinity): NearestNeighbour {
        let result = null
        if (!this.zones.length) {
            for (const el of this.elements) {
                if (p.distance(el) < distance && p !== el) {
                    result = el
                    distance = p.distance(el)
                }
            }
        } else {
            const sortedZones = [...this.zones]
                .sort((a, b) => a.area.distanceToPoint(p) - b.area.distanceToPoint(p))
            
            for (const zone of sortedZones) {
                if (zone.area.distanceToPoint(p) < distance) {
                    const el = zone.findNearestRec(p, distance)
                    if (el && p.distance(el) < distance) {
                        distance = p.distance(el)
                        result = el
                    }
                }
            }
        }
        return result
    }

The implementation above consists of 2 methods. The public method sets up our recursive method which requires extra parameter - our initial distance we are optimising for. This is additional parameter we need to pass to our recursive calls. If you want, you can expose this function - it will have additional ability of capping your maximum distance if you want to. Then you will find nearest neighour if it’s not further than distance. Our recursive function has 2 main cases: when there are no zones defined, then we are in a leaf node. In that case, we need to compare all elements and check if any element is closer than our distance. Otherwise we are in a node that is subdivided. In that case we visit our zones from the most promissing first. To do that we sort them by distance. Hopefuly we will find an element in a closer region and then we can ignore all regions which are further. For all regions which are still potentially closer than our minimal distance, we try visit them recursively. This will potentially result with an element that is closer than our initial one. If that’s the case, we can update our distance value.

Below is an interactive version for you to try out! The green point is the nearest neighour to your mouse pointer. Orange points are the points that were considered nearest at some point of the search. White regions are the visited leaf regions:

Next Steps

With this implementation we can easily get closest points to the user. This can be used in your game to detect enemies, check for collisions and much more. If you are looking for a challenge, try expanding this implementation with ability to tag the points added to quad-tree and then look for the nearest with a specific tag. Thanks to that you can look specifically for enemies or collectables in a given area and act differently on them. If you implement it, share your result on the Discord channel where we’re slowly building community around creative coding!

Getting Creative

You can also use quad-trees to get interesting visuals. The cover for this article connects closest points making it look like a star constellation. Try it out bellow. Click to generate new points and see constelation update:

Subscribe to Newsletter