Quad Trees: Find in the area

In the last article I introduced quad trees - a spatial data structure helping to quickly query elements in a 2-dimensional space. If you are not familiar with this data structure or want to refresh your knowledge, I recommend starting there:

Introduction to Quad Trees

Let's implement quad tree in TypeScript!

We previously implemented a basic algorithm to insert elements into the tree, which recursively split into separate quadrants when needed. However, a structure like this is pretty useless unless we can query the elements inside. In this article, we’ll learn how to efficiently fetch all the data in a given region.

Algorithm

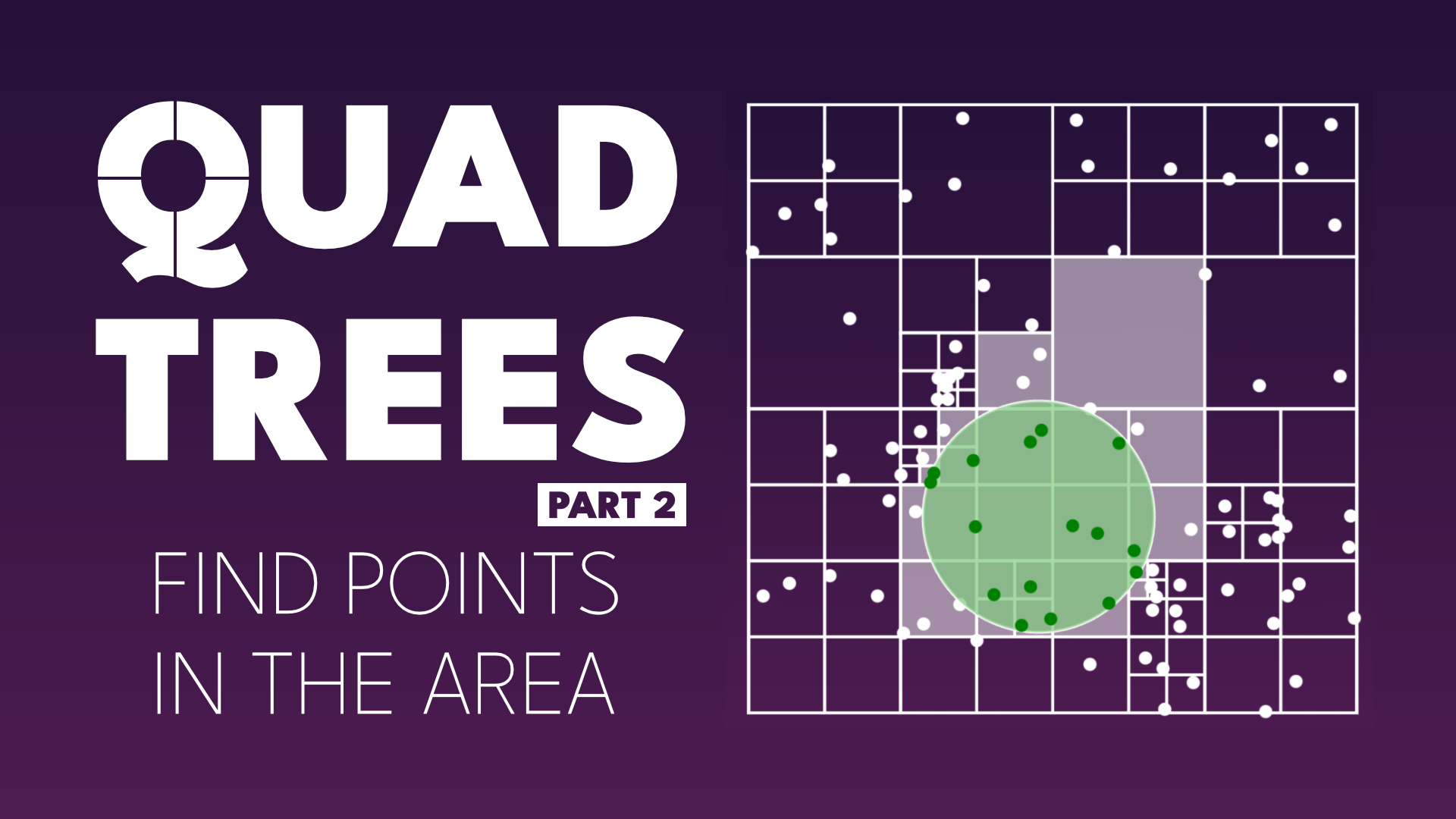
Before diving into implementation, let’s explore the algorithm we want to develop. Our goal is to retrieve all points from a specified area. While there are many ways to define the desired area - such as finding items within a certain radius or within a specific polygon - we’ll keep things straightforward by defining our area as a rectangle.

In our solution, we’ll traverse the quad tree from the root down. The key optimization is to skip areas that definitely don’t contain elements we’re looking for. We can safely ignore any area that doesn’t intersect with our area of interest. This simple insight forms the core of our solution!

We proceed recursively. If a quad tree node is divided into sub-quadrants, we visit only those subdivisions that intersect with our query region. For non-subdivided regions, we check each element individually to determine if it belongs to our target area. Thanks to the constraints of our quad tree, we won’t need to compare more than threshold elements in any single region. Once we’ve visited all relevant regions, we simply combine the results to produce our final solution.

Checking for intersections

The last piece missing in our implementation is a detailed algorithm for determining if two rectangles intersect. It turns out it’s easier to answer the opposite question: when do two rectangles not intersect? The answer is when one rectangle is either fully above, below, to the left, or to the right of the other. If you have trouble visualizing this concept, check this great visualisation created by Matthew Crumley.

Using De Morgan’s laws, we can convert this to our original question about intersection. De Morgan’s laws tell us that “not (A OR B OR C OR D)” is equivalent to “not A AND not B AND not C AND not D.” So if we negate each condition for non-intersection and combine them with AND operators, we get our intersection check, as shown in our code example:

class Rectangle {
    /* ... */
    intersects(r2: Rect) {
        return (
            this.p2.x >= r2.p1.x // not "fully to the left"
         && this.p1.x <= r2.p2.x // not "fully to the right"
         && this.p2.y >= r2.p1.y // not "fully above"
         && this.p1.y <= r2.p2.y // not "fully below"
        )
  }
}

Implementation

findInRange(r: Rect): Point[] {
      // Check if this node has been divided into quadrants
        if (this.zones.length) {
            return this.zones
                // Step 1: Filter out quadrants that don't intersect with our query rectangle
                .filter(z => r.intersects(z.area))
                // Step 2: Recursively search in each remaining quadrant
                .map(z => z.findInRange(r))
                // Step 3: Combine all points from all quadrants into a single array
                .flat()
        } else {
            // This is a leaf node - check each point individually
            return this.elements
                // Only return points that are within our query rectangle
                .filter(e => r.contains(e))
        }
    }

This recursive implementation turns out to be surprisingly concise, only a couple of lines long. We have two cases:

• If the area has been divided into quadrants (meaning we’re not at a leaf node), we filter out all regions that don’t intersect with our query region and run the method recursively on those that do. We need to flatten our results to end up with a flat array of values rather than separate arrays for each zone.
• If we’ve reached a leaf node, we need to examine each element in that region to determine if it belongs to our result set.

Demo

Check out live demo of our implementation.

Moving beyond rectangles

Now that we have our basic solution working with rectangles, let’s consider how we might extend this approach to handle more complex shapes.In the next section, we’ll explore how to adapt our quad tree to work with arbitrary shapes by creating a simple interface that any shape can implement.

Expanding the solution

Now that we have our basic solution ready, we can expand it to work with any arbitrary shape. Our function doesn’t really need to know what shape it’s looking for—it just needs to know if the desired shape intersects with a given rectangle and if a point is within it or not.

export interface Shape {
  intersects(r: Rect): boolean
  contains(p: Point): boolean
}

We can implement Circle class that implements this interface:

export class Circle implements Shape {
  constructor(public readonly center: Point, public readonly radius: number) { }

  contains(p: Point): boolean {
    const dx = this.center.x - p.x;
    const dy = this.center.y - p.y;
    const distance = Math.sqrt(dx * dx + dy * dy);

    // If the distance is less than or equal to the radius, the point is inside the circle
    return distance <= this.radius;
  }

  intersects(r: Rect): boolean {
    // Find the closest point on the rectangle to the circle's center
    const closestX = Math.max(r.p1.x, Math.min(this.center.x, r.p2.x));
    const closestY = Math.max(r.p1.y, Math.min(this.center.y, r.p2.y));

    return this.contains(new Point(closestX, closestY))
  }
}

The contains method uses the Pythagorean theorem to calculate the distance between the circle’s center and the point. If the distance is less than or equal to the radius, then the point must be within our circle.

To calculate intersection, we use the same method but determine the distance to the closest point on the rectangle’s edge. If this point is within the circle, then there must be an intersection between the rectangle and circle.

Conclusion

We’ve now completed our quad tree implementation with querying capabilities! This powerful data structure provides an efficient way to handle spatial queries, allowing us to quickly retrieve elements within a specified region. By implementing the algorithm recursively and using intersection checks to prune unnecessary branches, we’ve created a solution that scales well even with large datasets.

The flexibility of our approach also allows us to extend beyond simple rectangles to work with any arbitrary shape. As long as we can determine whether a shape contains a point and whether it intersects with a rectangle, we can use our quad tree to efficiently query it. This opens up numerous possibilities for applications in areas like geographic information systems, game development, and computer graphics.

If you want to expand on this solution, try implementing Polygon class that allows to check intersections with any arbitrary shape. Start by defining polygon as an array of points along the perimiter. This solution requires some more advanced linear algebra algorithms. If you manage to implement it or have questions about implementation, join my Discord channel to chat about it!

In the next article I will cover method how to find nearest neighbour of our element.

Subscribe to Newsletter