Counting in CSS: Unlock magic of CSS variables

element with no extra properties applied.

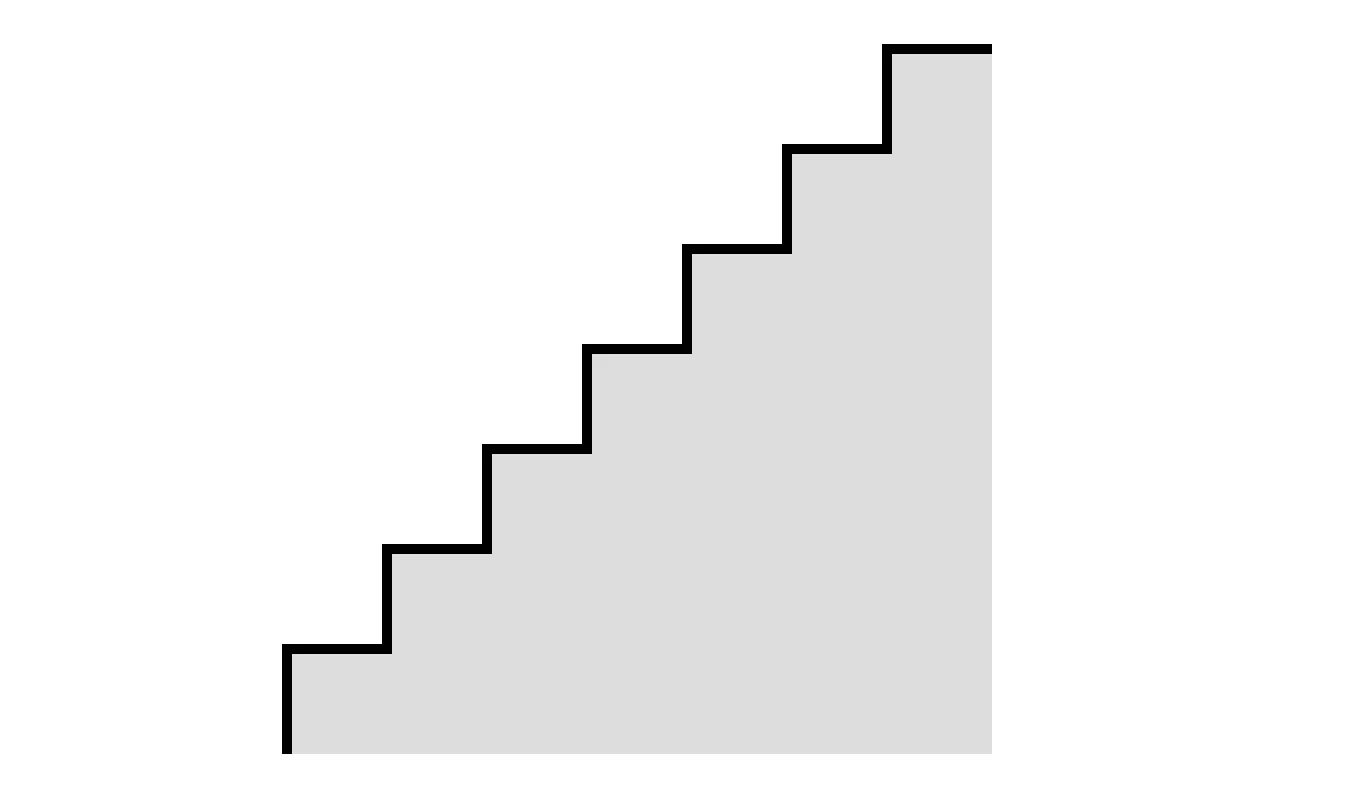
CSS operates in a context of a single element and does not have mechanisms to interact with or query its surroundings (the adjacent sibling combinators are very limited and won’t help us here). We also do not have a straightforward mechanism in CSS to get the ordinal of a given element (which in a sequence it is).

What about counters? #

You might have a hunch to look into CSS counters — they surely can do the trick, can’t they? Unfortunately, counter values cannot be assigned to variables nor used in calc equation. I did an experiment with counters but it turned out to be dead-end.

Naive solution #

Let’s try a naive solution first: we can just target each of the stairs separately and apply styling for it. Obviously, we’d have to repeat styles that change for each element making this solution pretty unportable.

See the Pen Stairs in CSS - Naive solution by hypersphere (@hypersphere) on CodePen.

The biggest drawback of the solution above is that we had to target each individual element with its separate selector and repeat styles for each of them.

There surely must be a better solution?

Below I present 2 approaches I’ve found — none of them is perfect and both have different drawbacks but they might be useful nevertheless.

Finding a better way — first attempt: binary! #

In the search for a better solution, I resorted to the basics of computer science. It turns out that in conjunction with nth-child we can use it to count our elements. If you are not familiar with binary, I will try to quickly explain it in the next section. If you think you know binary already, feel free to skip directly to the solution.

Introduction to binary system #

The binary system is the essence of our modern computing. All data are stored, transmitted and computed using its binary representation. There are many ways of encoding numbers to binary but, fortunately for us, in our case, we only operate on positive integers (whole numbers), which makes it possible to use the most simple representation. I have prepared Binary System 101 below to explain it (mind the pun):

The main building blocks of the binary system are 0-s and 1-s. Like in the decimal system we are used to, binary is positional — meaning that the position of a given zero or one in the sequence matters. The further to the left, the bigger part of the number it represents.

Unlike the decimal system, in which moving left increases by the factor of 10, in binary each movement doubles the value — for example 101 in binary represents 5 in decimal: 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 1 * 4 + 0 * 2 + 1 * 1 = 4 + 1 = 5.

Finding patterns #

To use our knowledge of binary system in CSS, we need to find a way to target specific bits — we want to write a selector that will match all numbers that should have specific bit set to 1 . Then we will set variables like b0, b1, b2, etc. to 1 only for the matching elements.

Let’s write first 16 numbers in binary (including 0 for consistency) and try to spot some patterns that would help us implement it in CSS. On the image below I highlighted all 1s — can you spot the pattern?

For each column, the pattern stays the same:

• The first column (from the right) has 1 set every other number.
• The second column (from the right) pattern alternates every 2 numbers.
• The next one alternates every 4 rows
• the next one 8, etc.

In general, the k-th column (indexing from 0) has sequence of 2^k bits off followed by 2^k bits on. We can use it in our CSS.

Binary counters in CSS #

Using that discovery we can write more generic nth-child selectors that will only match numbers that should have a specific bit set on. We can use CSS variables to set the bits. Then in the final selector, we can compute the actual counter value using the binary to decimal conversion.

:root {
  --b0: 0;
  --b1: 0;
  --b2: 0;
  --b3: 0;
  --b4: 0;
}

div:nth-child(2n) {
  --b0: 1;
}

div:nth-child(4n+3),
div:nth-child(4n) {
  --b1: 1;
}

div:nth-child(8n),
div:nth-child(8n-1),
div:nth-child(8n-2),
div:nth-child(8n-3) {
  --b2: 1;
}

div:nth-child(16n),
div:nth-child(16n-1),
div:nth-child(16n-2),
div:nth-child(16n-3),
div:nth-child(16n-4),
div:nth-child(16n-5),
div:nth-child(16n-6),
div:nth-child(16n-7) {
  --b3: 1;

}

div {
	--n: calc(var(--b0) + 2 * var(--b1) + 4 * var(--b2) + 8 * var(--b3));

	// Any CSS logic using --n can go here:
  height: calc(50px + 50px * var(--n));
}

The beauty of the solution is the fact that to represent the first 100 elements we only need 7 bits meaning 7 distinctive selector groups. That’s a big improvement compared to a naive solution that would need 100 separate classes. Moreover, we can automate it using SCSS mixins.

SCSS mixin #

If you use a CSS preprocessor like SCSS you can use the following mixing to achieve the same effect. It produces all required styles for user-defined depth. Because the selectors grow quite a bit with each step, for most cases we would probably want to stay below 8 which will still allow us to distinguish between 127 elements.

@mixin binaryCounter($selector: 'div', $bits: 4) {
  :root {
    @for $i from 0 to $bits {
      --b#{$i}: 0
    }
  }
  
  $exponent: 1
  $eq: "0"
  @for $i from 0 to $bits {
    $exponent: 2 * $exponent
    $eq: $eq + " + #{$exponent/2} * var(--b#{$i})"
    $sel: ""
    @for $j from 0 to $exponent/2 {
      $sel: $sel + "#{$selector}:nth-child(#{$exponent}n - #{$j}), "
    }
    #{$sel} {
        --b#{$i}: 1
      }
  }
  #{$selector} {
    --n: calc(#{$eq})
  }
}

// Usage
@include binaryCounter('div', 9)

You can see the use of the mixin below to generate 256 elements and style them individually.

See the Pen Binary counting in CSS - SCSS by hypersphere (@hypersphere) on CodePen.

Drawbacks #

Unfortunately, after closer analysis of the code you can realise that we are still generating a lot of code. We no longer have individual styles for each element, instead we have only few (to be technical ceil(log2(n)) for any given maximal n elements we want to distinguish but each of those groups have exponentially more coma-separated selectors. We still end up with many selectors.

In a search of a better solution: prime numbers #

After the first failed attempt, I tried a different approach. What if instead of splitting a number into its binary bits, we would try to use its prime factors. As a refresher, below’s the Prime Numbers Primer:

Unfortunately computing just prime numbers and making groups out of them is not enough. Some numbers are made out of the same prime factor combined: 4 is the smallest example — it’s prime factors are 2 * 2. With that in mind I created a mixin that generates prime groups and their powers up to the given threshold:

@function isPrime($n, $primesList) {
  @each $prime in $primesList {
    @if ($n % $prime == 0) {
      @return false;
    }
  }
  @return true;
}

@mixin primeCounter($selector, $upperBound: 2000) {
  
  $curr: 2;
  $primesList: [];
  
  @while $curr <= $upperBound {
    @if isPrime($curr, $primesList) {
      $primesList: append($primesList, $curr);
    }
    $curr: $curr + 1;
  }
  :root {
    @each $prime in $primesList {
        --p#{$prime}: 1;
    }
  }
  $mult: "1";
  @each $prime in $primesList {
    $mult: $mult " * var(--p#{$prime})";
    $val: $prime;
    @while $val <= $upperBound {
      #{$selector}:nth-child(#{$val}n) {
        --p#{$prime}: #{$val};
      }
      $val: $val * $prime;
    }
  }
  
  #{$selector} {
    --n: calc(#{$mult});
  }
}

// Example use
@include primeCounter("div", 500);

Below you can see an example with the threshold set to 500. Notice that up to the threshold all the numbers are perfectly fine but above that the pattern breaks. All prime numbers above would default to 1 as they were not computed. Some composite numbers might miss one or few of its factors resulting in the number being smaller than expected. But for plenty of values, we can still see proper results.

The solution to generate properly first 500 numbers required 114 separate selectors — it’s a great improvement on both naive and binary solutions. Moreover, it still provides a lot of value for the elements above the threshold and can be useful in cases like generative art where we might not care too much about the exact values.

See the Pen Counting in CSS: Primary Counter by hypersphere (@hypersphere) on CodePen.

Use-cases #

There are multiple use-cases for being able to distinguish between identical elements and being able to process them differently. I came up with a few, but I would like to hear more from you in the comments about what other ideas you might have! Here are couple of mines:

Staircase #

First, let’s finish out the staircase example. Using this technique we can write more generic code to achieve the same effect.

See the Pen Binary counters in CSS - stairs by hypersphere (@hypersphere) on CodePen.

Generative art #

Generative art is an amazing example where CSS can be incorporated. There are plenty of great CSS artists out there but all the examples I could find use at least some JavaScript to either number the elements or add randomness to the stylesheet. All the examples here do not use any JavaScript at all.

See the Pen Binary Counter in CSS - Generative Art 1 by hypersphere (@hypersphere) on CodePen.

Great thing about this technique is that you can use the ordinal number inside the animations too. Each element will use it’s own value making it possible to implement very interesting effects:

See the Pen Untitled by hypersphere (@hypersphere) on CodePen.

We can also use @property to define and animate variable to create interesting rotating effects like this vortex-like creation. In the browsers that do not support @property the image will appear static providing a graceful fallback. This example also uses a prime generator set to 250 threshold despite utilising 500 elements to show that even less accurate, the values above the threshold can give us really interesting patterns too.

Because of use of @property the animation works only in Chrome but in other browsers the static version is shown.

See the Pen Generative Art: Rotating Sphere by hypersphere (@hypersphere) on CodePen.

What is your take on this solution? Do you know any examples where having ordinal numbers for elements would be helpful?